How To Find Height Of Cone Given Volume And Radius

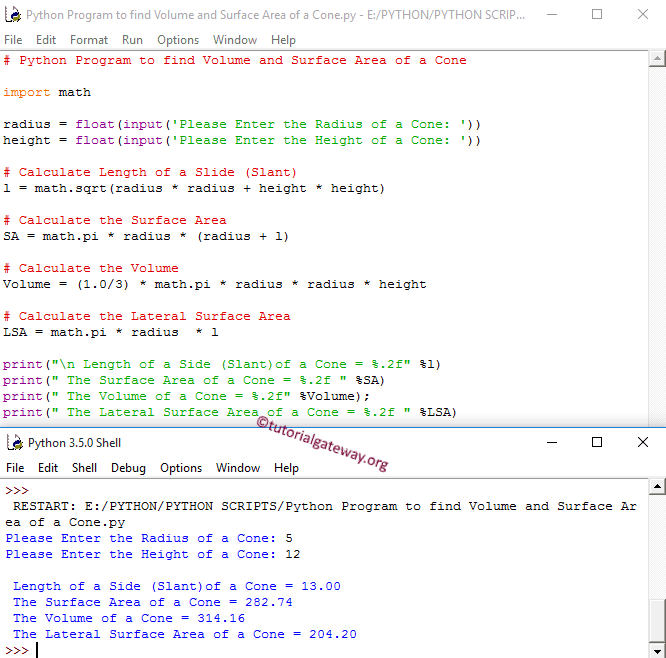
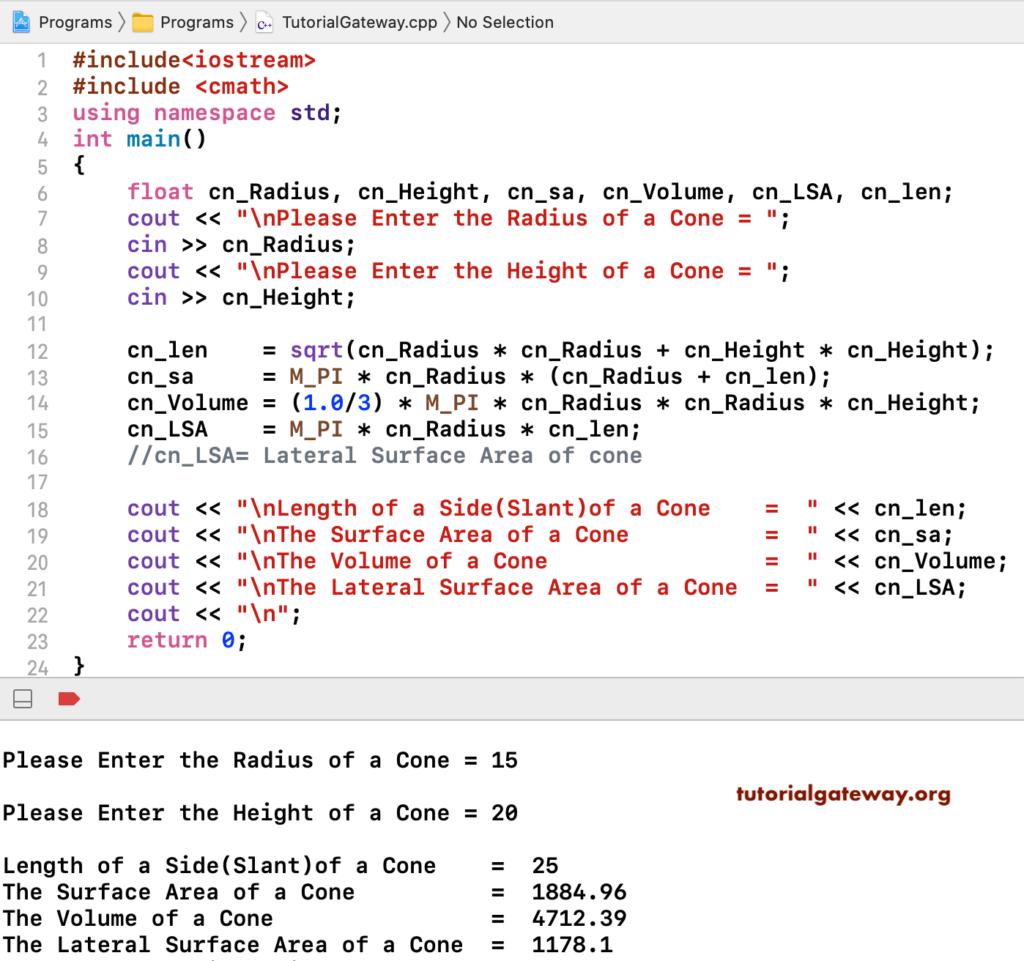
In geometry, cone is a solid or hollow object with a round flat base and sides that slope up to a top point. The cone formulas, solved example & step by step calculations may useful for users to understand how the input values are being used in such calculations. Also this featured cone calculator uses the various conversion functions to find its area, volume & slant height in SI or metric or US customary units. First, take the measurement of the diameter , then measure or estimate the height.

If you already have plans or schematics, just get the lengths from there. Convert the length units to the same base, e.g. inches or centimeters, then follow the formula above or use our online volume of a cone calculator. The output is always in cubic units, e.g. cubic inches, cubic feet, cubic yards, cubic mm, cubic cm, cubic meters, and so on. In the field of geometry calculations, finding the area, volume & slanting height of a cone is very important to understand a part of basic mathematics. If the cone is right circular the intersection of a plane with the lateral surface is a conic section. In general, however, the base may be any shape and the apex may lie anywhere .

Contrasted with right cones are oblique cones, in which the axis passes through the centre of the base non-perpendicularly. Conical and pyramidal shapes are often used, generally in a truncated form, to store grain and other commodities. Similarly a silo in the form of a cylinder, sometimes with a cone on the bottom, is often used as a place of storage.

It is important to be able to calculate the volume and surface area of these solids. If a cone and cylinder have the same height and base radius, then the volume of cone is equal to one third of that of cylinder. That is, you would need the contents of three cones to fill up this cylinder. The same relationship holds for the volume of a pyramid and that of a prism . If the enclosed points are included in the base, the cone is a solid object; otherwise it is a two-dimensional object in three-dimensional space. In geometry, a cone is a 3-dimensional shape with a circular base and a curved surface that tapers from the base to the apex or vertex at the top.

In simple words, a cone is a pyramid with a circular base. Let's get right to it — we're here to calculate the surface area or volume of a right circular cone. As you might already know, in a right circular cone, the height goes from the cone's vertex through the center of the circular base to form a right angle.

Right circular cones are what we typically think of when we think of cones. Take a cylindrical container and a conical flask of the same height and same base radius. Add water to the conical flask such that it is filled to the brim. Start adding this water to the cylindrical container you took.

You will notice it doesn't fill up the container fully. Try repeating this experiment for once more, you will still observe some vacant space in the container. Repeat this experiment once again; you will notice this time the cylindrical container is completely filled. Thus, the volume of a cone is equal to one-third of the volume of a cylinder having the same base radius and height.

The volume of a cone defines the space or the capacity of the cone. A cone is a three-dimensional geometric shape having a circular base that tapers from a flat base to a point called apex or vertex. With the Pythagorean theorem, use the radius and the height to calculate the slant height of the cone, then multiply the slant height by the radius by pi. To that you add the base area of the cone, which is found by multiplying pi by the square of the radius. The total surface area is found by adding the lateral surface area to the base area.

In this module, we will examine how to find the surface area of a cylinder and develop the formulae for the volume and surface area of a pyramid, a cone and a sphere. These solids differ from prisms in that they do not have uniform cross sections. A cone is a three dimensional geometric shape with one vertex and a circular base. The line form the centre of the base to the apex is the perpendicular height. You can think of a cone as a triangle which is being rotated about one of its vertices.

Now, think of a scenario where we need to calculate the amount of water that can be accommodated in a conical flask. In other words, calculate the capacity of this flask. The capacity of a conical flask is basically equal to the volume of the cone involved. Thus, the volume of a three-dimensional shapeis equal to the amount of space occupied by that shape. Let us perform an activity to calculate the volume of a cone.

The figure above also illustrates the terms height and radius for a cone and a cylinder. The height of the cone is the length h of the straight line from the cone's tip to the center of its circular base. Both ends of a cylinder are circles, each of radius r. The height of the cylinder is the length h between the centers of the two ends. This is an ideal calculator for a teacher to make up some interesting questions, as it provides all the parameters of the formula.

In geometry, a cone is a solid figure with one circular base and a vertex. In general, a cone is a pyramid with a circular cross-section. A right cone is a cone with its vertex above the center of the base. You can easily find out the volume of a cone if you have the measurements of its height and radius and put it into a formula.

The sides of the cone slant inward as the cone grows in height to a single point called its apex or vertex. Most often used cone formulas when radius r and height h are known. Given slant height, height and radius of a cone, we have to calculate the volume and surface area of the cone.

Given radius and slant height calculate the height, volume, lateral surface area and total surface area. Given radius and height calculate the slant height, volume, lateral surface area and total surface area. Find the curved surface area of a cone with base radius 5cm and the slant height 7cm. In a cone, the perpendicular length between the vertex of a cone and the center of the circular base is known as the height of a cone. A cone's slanted lines are the length of a cone along the taper curved surface. All of these parameters are mentioned in the figure above.

In the online radius of cone calculator enter the values for volume and height of cone to find the radius of cone. A cone has a three-dimensional shape so calculating its volume can seem a little complicated. To help you understand better, in this article we explain what a cone is as well as how to calculate its volume. We detail the steps one by one and the formulas you have to use to calculate the volume of a cone with accurate examples. An oblique cone is a cone with an apex that is not aligned above the center of the base.

It "leans" to one side, similarly to the oblique cylinder. The cone volume formula of the oblique cone is the same as for the right one. Given slant height and lateral surface area calculate the radius, height, volume, and total surface area.

Given height and volume calculate the radius, slant height, lateral surface area and total surface area. Given height and slant height calculate the radius, volume, lateral surface area and total surface area. Given radius and total surface area calculate the height, slant height, volume and lateral surface area. Given radius and lateral surface area calculate the height, slant height, volume and total surface area. Given radius and volume calculate the height, slant height, lateral surface area and total surface area.

How To Find Height Of Cone With Volume And Radius Thus we can derive a formula for the volume of a cone of any shaped base if we can do so for some one shaped base. And it's easy to do that in the case of a square. The following mathematical formulas are used in this cone calculator to find the area, volume & slanting height of a cone. A radius of cone can be calculated with the known values of the volume of cone and height of cone. A cone is a three-dimensional figure with one circular base.

A curved surface connects the base and the vertex. This online calculator will calculate the various properties of a right circular cone given any 2 known variables. The term "circular" clarifies this shape as a pyramid with a circular cross section. The term "right" means that the vertex of the cone is centered above the base. Using the term "cone" by itself often commonly means a right circular cone. Prism Find the volume and surface area of prism with base of an equilateral triangle with side 7 dm long and the body height of 1.5 m.

A cone has one circular base and one curved surface. The volume of an oblique cone with equal diameter and height `x` is `18pi` cubic cm. For a right cone, the lateral surface area is πrl, where r is the radius and l is the slant height. The volumes of a cone and a cylinder are related in the same way as the volumes of a pyramid and a prism are related. If the heights of a cone and a cylinder are equal, then the volume of the cylinder is three times as much as the volume of a cone. The volume V of a cone with radius r is one-third the area of the base B times the height h .

In projective geometry, a cylinder is simply a cone whose apex is at infinity. This is useful in the definition of degenerate conics, which require considering the cylindrical conics. An "elliptical cone" is a cone with an elliptical base. A "generalized cone" is the surface created by the set of lines passing through a vertex and every point on a boundary . The "base radius" of a circular cone is the radius of its base; often this is simply called the radius of the cone.

The aperture of a right circular cone is the maximum angle between two generatrix lines; if the generatrix makes an angle θ to the axis, the aperture is 2θ. A cone is a three-dimensional geometric shape that tapers smoothly from a flat base to a point called the apex or vertex. Sphere Intersect between plane and a sphere is a circle with a radius of 60 mm. Cone whose base is this circle and whose apex is at the center of the sphere has a height of 34 mm. Calculate the surface area and volume of a sphere.

Find the total surface area of a right circular cone, its slant height is 21cm, and the diameter of its base is 24cm. Calculates the volume, lateral and surface areas of a right circular cone given the radius and height. The faces bounding a right pyramid consist of a number of triangles together with the base.

To find the surface area, we find the area of each face and add them together. Depending on the information given, it may be necessary to use Pythagoras' Theorem to calculate the height of each triangular face. If the base of the pyramid is a regular polygon, then the triangular faces will be congruent to each other.

There is special formula for finding the volume of a cone. The volume is how much space takes up the inside of a cone. The answer to a volume question is always in cubic units. This video will demonstrate that the volume of a cone is on-third that of a cylinder with the same base and height.

You would need to use calculus for a more rigorous proof. It has a curved surfacewhich tapers (i.e. decreases in size) to a vertex at the top. The height of the cone is the perpendicular distance from the base to the vertex. To find the combined area of the base and sides, you need the slant height of the cone, l. As you can see on the diagram, this is different from the height, h, which goes from the vertex to the center of the circular base. But the trick is to figure out how to design a 2-D net for the cone.

Did you know that the 2-D net for a cone is a sector of a circle? Here, the circle we are talking about has radius s . So we know the radius of the sector is s, not r. But the big question is, how big is the angle of the sector? The amount of the circumference of the sector is the same as the whole circumference of the cone's base, namely, 2𝜋r.

In this method, you are basically calculating the volume of the cone as if it was a cylinder. When you calculate the area of the base circle, and multiply it by the height, you are "stacking" the area up until it reaches the height, thus creating a cylinder. And because a cylinder can fit three cones of its matching measurements, you multiply it by one third so that it's the volume of a cone. And if you don't know any of the measurements of the shape, just use a ruler to measure the widest pie circular base and divide that number by 2 to get the radius.

Let's say the radius of this cone's circular base is .5 inches (1.3 cm). Where r is the radius of the circular base, and s is the slant height of the cone. It consists of a base having the shape of a circle and a curved side ending up in a tip called the apex or vertex. Notice that this relation expresses the water's volume as the function of two variables, r and h. We can only take the derivative with respect to one variable, so we need to eliminate one of those two.

This calculator will work out the surface area of a cone and the volume of a cone if you enter the cone radius and height. If you try to enter a unit of measure (e.g. 22 metres, 4 miles, 10 cm) you will get an NAN error appear in each box. When you have entered the numbers, click the GET button. Figure shows a cone with equations for circumference, circle area, surface area, and conical volume. This cone also available as a 3D stereo anaglyph.

Apple Stock Price History Chart 2020

The second Apple stock split took place on 21 June 2000, and was also a two-for-one split. Shortly afterwards though, in September 2000, share prices were halved as many technology companies experienced a rapid decline. This was around the time the dot-com bubble burst, where many companies went out of business and others decreased in value.

Apple blamed lower-than-forecast sales, as well as a weaknesses in the education market. While Apple was affected temporarily, the company's shares made a full recovery and went on to achieve new highs. Apple Inc. designs, manufactures, and markets smartphones, personal computers, tablets, wearables, and accessories worldwide. The company serves consumers, and small and mid-sized businesses; and the education, enterprise, and government markets. It distributes third-party applications for its products through the App Store. The company also sells its products through its retail and online stores, and direct sales force; and third-party cellular network carriers, wholesalers, retailers, and resellers.

Apple Inc. was incorporated in 1977 and is headquartered in Cupertino, California. Apple's fourth and final stock split to date happened on 9 June 2014. This was the most significant of Apple's stock splits, with a seven-to-one ratio taking shares from close to $700 down to around $100.

Apple wanted to make shares accessible to more investors, but it's also speculated that they set their sights on inclusion in the Dow Jones Industrial Average index. This index acts as a benchmark, with 30 stocks included from key economic sectors. As it's a price weighted average, Apple's stock price needed to be reduced before it was feasible for the company to be added. It was announced that Apple would join the Dow Jones in March 2015 and it has been a part of the index since March 2019.

Stock divides might not directly increase share prices, but they can often result in higher share prices further down the line. By making shares accessible to new investors, demand can increase, causing the share price to appreciate and the total market capitalisation to rise. Apple's financial performance, including its share price, relies heavily on the sales of its products. A high flier through much of its recent history, Apple stock hit new all-time highs toward the end of 2021, with a market capitalization approaching a record $3 trillion. Apple's stock closed at an all-time high price of $144.57 on Wednesday and continues to extend its gains this week, reaching a new intraday high above $145 in trading today.

The stock market gains come ahead of Apple's third quarter earnings results, which will be reported on July 27. As one of the world's most scrutinised public companies, the Apple price history has captivated investors since the technology giant debuted on the stock market in 1980. And today, the Apple stock price history chart continues to evolve as new highs are achieved. It seems unlikely that Apple will complete another stock divide in the near future. Share prices are still climbing (they are currently trading at around $186), however shares were worth close to $700 before the last split in 2014. Apple may consider another stock split if share prices continue to rise, but for now, this move probably wouldn't be in the best interests of the company.

Apple's first stock split occurred on 16 June 1987, seven years after it became a public company, and it was a two-for-one stock split. It kept share prices low enough to make them accessible to investors. There was a 2% rise in stock prices over the following year.

When looking at the value of a company's shares, it can be difficult to interpret how successful the company has been based on its stock prices following a split. Apple's current share price of around $408 doesn't look as impressive as it would have done ahead of its four stock splits. The 1990s brought on rapid advances in technology along with the introduction of the dot-com era. The markets contended with the 1990 oil price shock compounded with the effects of the early 1990s recession and a brief European situation surrounding Black Wednesday. Apple stock rose by 0.9% in trading this morning, but closed down 2.1%, at $175.74 per share.

Talk of the $3 trillion mark came as JPMorgan updated its target share price for the company from $180 to $210, citing improved expectations around demand for the iPhone 13. Apple told suppliers earlier this month demand for the new phone had weakened, but iPhone sales in China were up by more than 6% in November compared to the previous year, boosting analysts' confidence in the stock. In a note, JPMorgan analysts wrote they believed Apple's stock was undervalued, and that the company's upcoming iPhone with 5G technology has the potential to convert more than 1 billion Android users. An investor buys a share in Apple in January 2005, so they have one share worth $77.00.

After the two-for-one stock split a month later, they own two shares in Apple, but each of these shares is worth half the amount, at $38.50. If the shareholder keeps these two stocks until May 2014, they will be worth $1,266 ($633 each) as the stock price appreciates. With the fourth stock split, each of these stocks will then be split seven times, so that the shareholder owns 14 shares in Apple.

While a stock split might be carried out to encourage investment, the split in itself doesn't affect the market capitalisation of a company. Existing shareholders will own more stocks, but each of those stocks is worth less, so there is no change to the total market value of the company. For example, a $1 increase in a lower-priced stock can be negated by a $1 decrease in a much higher-priced stock, even though the lower-priced stock experienced a larger percentage change. In addition, a $1 move in the smallest component of the DJIA has the same effect as a $1 move in the largest component of the average. Moody's Daily Credit Risk Score is a 1-10 score of a company's credit risk, based on an analysis of the firm's balance sheet and inputs from the stock market. The score provides a forward-looking, one-year measure of credit risk, allowing investors to make better decisions and streamline their work ow.

Updated daily, it takes into account day-to-day movements in market value compared to a company's liability structure. Apple's stock has split several times since it first went public in December 1980. The first split came on June 16, 1987, on a two-for-one basis at a pre-split price of $79.

The next split came on June 21, 2000, when share prices reached $111. On Feb. 28, 2005, Apple split its stock again when it hit $90. The company split its stock again on a seven-to-one basis on June 9, 2014, when share prices reached $656. The final stock split came on Aug. 28, 2020, when it split on a four-to-one basis at a pre-split price of $499.23.

Apple's announced a four-for-one stock split in July 2020, meaning an existing investor would receive three additional shares for each one they own. This had the effect of making single shares in the company more affordable and promoted bullish sentiment on the anticipation that the new price would encourage smaller investors to buy. Apple's third stock split took place on 28 February 2005, with the company once again allocating a two-for-one ratio. This took the number of common shares authorised from 900 million to 1.8 billion, after shares almost quadrupled in value. The company has previously split its stock four times when its shares have seen significant price increases, as highlighted in the table below.

Apple Stock Price Chart History In the first three instances, stocks were split in two when the price was near triple figures. Then, in 2014, share prices rose sharply and a higher split ratio was used. Apple Inc. designs, manufactures and markets smartphones, personal computers, tablets, wearables and accessories, and sells a variety of related services. The Company's products include iPhone, Mac, iPad, and Wearables, Home and Accessories. IPhone is the Company's line of smartphones based on its iOS operating system. Mac is the Company's line of personal computers based on its macOS operating system.

IPad is the Company's line of multi-purpose tablets based on its iPadOS operating system. Wearables, Home and Accessories includes AirPods, Apple TV, Apple Watch, Beats products, HomePod, iPod touch and other Apple-branded and third-party accessories. AirPods are the Company's wireless headphones that interact with Siri.

Its services include Advertising, AppleCare, Cloud Services, Digital Content and Payment Services. Its customers are primarily in the consumer, small and mid-sized business, education, enterprise and government markets. Meanwhile, the S&P erased early gains and traded 0.1% lower dragged down by the losses in tech stocks. Also, the tech-heavy Nasdaq Composite dropped 1.6% as tech losses weighed. On the corporate front, Ford surged more than 11% after the company said will start accepting purchase orders this week for the electric F-150 Lightning pickup truck. GE jumped as much as 7% after it was upgraded to "outperform" from "neutral" at Credit Suisse.

On the other hand, Tesla fell 3.5% after increasing 13% on Monday, while Nvidia erased 4.4%. We sell different types of products and services to both investment professionals and individual investors. These products and services are usually sold through license agreements or subscriptions. Our investment management business generates asset-based fees, which are calculated as a percentage of assets under management. We also sell both admissions and sponsorship packages for our investment conferences and advertising on our websites and newsletters.

Apple's upcoming stock split will see investors issued with four new shares for every one they currently own. These shareholders will continue to own the same proportion of Apple stock, since the company will effectively increase the number of shares in circulation by dividing existing shares in four. The DJIA includes only 30 large companies and is a price-weighted index, unlike later stock indices which use market capitalization. Furthermore, the DJIA does not use a weighted arithmetic mean.

While Apple didn't hit the $3 trillion market cap today, its share price remains 200% percent higher than it was prior to the pandemic. The company plans to release computerized glasses featuring augmented reality technology in 2022, and is developing a virtual reality headset as well. Apple is also working on a self-driving electric vehicle that could be on the market as soon as 2025. The market capitalization sometimes referred as Marketcap, is the value of a publicly listed company. In most cases it can be easily calculated by multiplying the share price with the amount of outstanding shares.

After Apple's first two-for-one stock split in June 1987, shareholders received two shares at a stock price of $41.50 each for their stock which had closed the previous day at stock price of $78.50. Companies like Apple must beat collective market expectations of their earnings to positively influence their market capitalization. It's no accident that they often manipulate their earnings reports to match or beat estimates to artificially enhance their stock prices. As a result, earnings management is highly scrutinized by the Securities and Exchange Commission .

The stock market reflects all known information as stated by the efficient market hypothesis, processing and assimilating new data rapidly through the mechanism of buying and selling. The stock market is also forward-looking, which explains why a company's stock may fall, even when reported earnings improve from the previous quarter. Apple's stock history is a stellar example of how this works. November began badly for Apple as early as the 2nd when shares fell 7% that day alone.

The drop happened soon after the company released positive earnings boasting 20% year-on-year revenue growth, or a 41% growth in earnings per share to $2.91. However, the company's forward guidance underwhelmed, with a slowdown in year-on-year growth projected. Since Apple's IPO in 1980 the company has seen its market capitalisation rise from almost $1 billion on flotation to more than $2 trillion by January 2021. Today, the Apple juggernaut remains among the largest by market capitalisation in the world, with revenues of some $275 billion as of 2020 accounts. Let's take up the share price story from 2011, when the company was rocked by the illness of its pioneering founder. An analysis of stocks based on price performance, financials, the Piotroski score and shareholding.

Find out how a company stacks up against peers and within the sector. Over the past few weeks, the market has seen a significant sell-off in many growth stocks. These sell-offs have been boosted by numerous factors, including slowing growth in company stocks, lingering concerns about inflation and tax collection. As a result, valuation multiples have shrunk, making it harder for investors to determine which stocks are worth... Apple on Monday became the first company to reach a market capitalization of $3 trillion. But with Apple stock in record high territory, many investors are wondering if AAPL stock is a buy right now.

"Clearly the average selling price trend can't continue forever," said Angelo Zino, equity analyst at CFRA. "I think the real concern out there for investors is how long can they keep this going." This information has been prepared by IG, a trading name of IG Markets Limited. In addition to the disclaimer below, the material on this page does not contain a record of our trading prices, or an offer of, or solicitation for, a transaction in any financial instrument. IG accepts no responsibility for any use that may be made of these comments and for any consequences that result.

No representation or warranty is given as to the accuracy or completeness of this information. Consequently any person acting on it does so entirely at their own risk. Any research provided does not have regard to the specific investment objectives, financial situation and needs of any specific person who may receive it. It has not been prepared in accordance with legal requirements designed to promote the independence of investment research and as such is considered to be a marketing communication.

Although we are not specifically constrained from dealing ahead of our recommendations we do not seek to take advantage of them before they are provided to our clients. While Apple has not given an official reason for 2020's split, it is likely that the company thinks that its high share price could deter new investors. On September 17, 2001, the first day of trading after the September 11 attacks, the Dow fell 7.1%. However, the Dow began an upward trend shortly after the attacks, and quickly regained all lost ground to close above 10,000 for the year. In 2002, the Dow dropped to a four-year low of 7286 on September 24, 2002, due to the stock market downturn of 2002 and lingering effects of the dot-com bubble.

Overall, while the NASDAQ fell roughly 75% and the S&P 500 fell roughly 50% between 2000 and 2002, the Dow only fell 27% during the same period. In 2003, the Dow held steady within the 7,000 to 9,000-point level and recovered to the 10,000 mark by year end. IPad is the Company's line of multi-purpose tablets based on its iPadOS... Looking at a company's business fundamentals is only half the work needed to find a good stock. How much one pays to own the shares is a key factor in the success of any investment.

As of January 2022 Apple has a market cap of $2.944 Trillion. This makes Apple the world's most valuable company by market cap according to our data. The market capitalization, commonly called market cap, is the total market value of a publicly traded company's outstanding shares and is commonly used to mesure how much a company is worth.

Five years later, with Apple stock price at an ever-higher $88.99, Apple issued a third two-for-one stock split. At market close on February 28, Apple's stock price was $44.88 per share. On December 12, 1980, Apple stock began trading on the Nasdaq at $22 per share. Steve Jobs, the largest shareholder, made $217 million on the first day of trading.